复杂性科学的核心问题是:涌现和自组织行为是如何产生的
- 简单规则以难以预测的方式产生出复杂行为,这种系统的宏观行为有时也称为涌现
- 系统有组织的行为不存在内部和外部的控制者或领导者,则也称之为自组织(self-organizing)
混沌的动力学方程
牛顿力学描绘了一幅“钟表宇宙”的图景:设定好初始状态,然后就遵循着三条定律一直运行下去。数学家拉普拉斯认识到其中蕴含了可以如钟表般精准预测的观念:他在1814年断言,根据牛顿定律,只要知道宇宙中所有粒子的当前位置和速度,原则上就有可能预测任何时刻的情况。[插图]在20世纪40年代计算机被发明出来之后,这种“原则上”的可能似乎有可能变成现实了。
早期牛顿在物理科学的进步,发展出来了”决定论”.
决定论
决定论认为万事万物都由物理定律决定,每一件事情之间遵循严格的因果规律。
早期人们认为不存在真正的随机数,计算机里也不存在真正的随机数。计算机生成的所谓随机数,实际上是取一个现成的数字(比如系统时间),经过一系列固定公式计算出来的。
决定论带来的问题
- 人类没有了自由意志;因为意识是由我们身体物质组成的,物质遵循物理定律。
- 没有自由,意味着不需要负责,带来人的虚无
#example# 追乌龟的芝诺就是一个决定论者
芝诺平时总念叨着一切都是注定的。结果有一次,他的奴隶犯了错误,他就鞭挞那奴隶作为惩罚。但是他的奴隶很聪明,辩解说:主人,按照你的决定论学说,我犯错是天生注定了的,不是我自己能控制的,所以你不应该惩罚我。然而芝诺更聪明,他回答说:你说的没错。但是按照同样的理论,我鞭挞你也是天注定了的。所以你就挨打吧。
古希腊的斯多葛学派相信部分决定论。他们认为我们不能控制事物,但是可以控制我们自己对待生活的方式。所以这个学派提倡随遇而安的生活态度。
但是混沌系统以及量子力学的出现给这种绝对的因果论,带来了致命一击。
混沌定义
混沌指的是一些系统——混沌系统——对于其初始位置和动量的测量如果有极其微小的不精确,也会导致对其的长期预测产生巨大的误差。也就是常说的“对初始条件的敏感依赖性”
三体问题
庞加莱在试图解决一个比预测飓风简单得多的问题时发现了对初始条件的敏感依赖性。他试图解决的是所谓的三体问题(three-body problem):用牛顿定律预测通过引力相互作用的三个物体的长期运动。牛顿已经解决了二体问题。但没想到三体问题要复杂得多。在向瑞典国王表示敬意的一次数学竞赛中,庞加莱将其解决了。竞赛主办方提供2500瑞典克朗奖励解决“多体”问题:用牛顿定律预测任意多个相互吸引的物体的未来运动。提出这个问题是为了确定太阳系是否稳定,行星是会维持还是会偏离目前的轨道?庞加莱想先试着解决三体问题。 #example# #math#
混沌系统中初始的不确定性到底是如何被急剧放大的呢?关键因素是非线性。非线性系统中总体不等于部分之和。
#example# 举个例子,将一堆兔子分成两部分,放到两个岛上,如果岛上的资源受限制,用逻辑斯蒂模型(logistic model)描述这种情形下群体数量的增长。这个模型以一种简化方式描述群体数量的增长。你设定好出生率、死亡率(由于种群数量过多导致的死亡概率)以及最大种群承载能力(栖息地所能承载的种群数量上限)。 这样兔子一年之后的总数在分成两堆,和不分成两队的总数是不一样的。
逻辑斯蒂映射
$$
x_{t+1}=R x_{t}\left(1-x_{t}\right)
$$
R取不同的值最终x收敛情况差别很大。
随着R增加,x从不动点,到二周期震荡,四周期震荡,直到发散,
逻辑斯蒂映射还被用来在计算机中生成伪随机数。因此,表面上的随机可以来自非常简单的确定性系统。
简单总结如下
- 即逻辑斯蒂映射能产生类似于随机噪声的确定性轨道,这个事实有着让人困扰的实际含义。例如,这就意味着种群调查数据中那种明显的不稳定波动不一定表明环境的变化莫测或是采样有错误
- 在混沌中,不管初始条件有多接近,在足够长的时间之后,它们的轨道还是会相互分开。这意味着,即使我们的模型很简单,所有的参数也都完全确定,长期预测也仍然是不可能的。
混动的共性
- 单峰映射存在倍周期
- 周期倍增速度为常数:新的周期倍增比前面的周期倍增出现的速度快大约4.6692016倍
小结
看似混沌的行为有可能来自确定性系统,无须外部的随机源。一些简单的确定性系统的长期变化,由于对初始条件的敏感依赖性,即使在原则上也无法预测。虽然混沌系统的具体变化无法预测,在大量混沌系统的普适共性中却有一些“混沌中的秩序”,例如通往混沌的倍周期之路,以及费根鲍姆常数。因此虽然在细节上“预测变得不可能”,在更高的层面上混沌系统却是可以预测的。
信息
我们讨论自组织,实际上是一个从无序到有序过程,一个熵减少过程,复杂系统科学最关注的问题就是这种逆熵的自组织系统是如何可能的。
第二定律:熵总是不断增加直至最大。系统总的熵会不断增加,直至可能的最大值;除非通过外部做功,否则它自身永远也不会减少。热力学第二定律是唯一区分过去和未来的基本物理定律。其他物理定律在时间上都是可逆的。
熵的新定义
玻尔兹曼将宏观状态的熵定义为其对应的微观状态的数量。 这极大撇清了我的疑惑,以前认为熵只是关于能量,温度的关联, 新的定义将熵转化为了信息的度量。
麦克斯韦的思想实验
麦克斯韦假设有一个箱子被一块板子隔成两部分,板子上有一个活门,如图所示。活门有一个“小妖”把守,小妖能测量气体分子的速度。对于右边来的分子,如果速度快,他就打开门让其通过,速度慢就关上门不让通过。对于左边来的分子,则速度慢的就让其通过,速度快的就不让通过。一段时间以后,箱子左边分子的速度就会很快,右边则会很慢,这样熵就减少了。麦克斯韦假设了小妖使用的门既无质量也无摩擦,因此开门关门要不了多少功,可以忽略不计(对这种门提出了可行的设计)
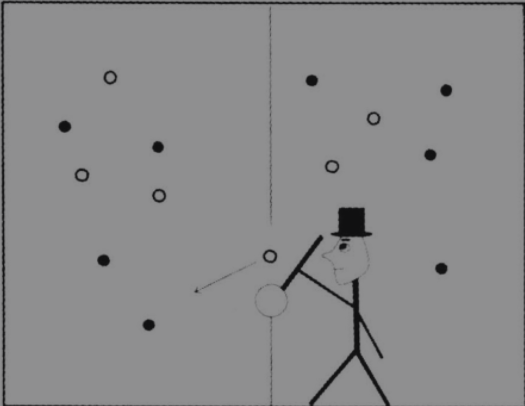
这个悖论如何解释呢?
小妖要通过测量获取“比特”信息,比如趋近的分子速度是慢是快,需要能量,因此必然会产生一定的熵,数量不少于分子变得有序而减少的熵。这样由箱子、分子和小妖组成的整个系统就仍然遵守热力学第二定律。
计算
希尔伯特提出了一系列的数学问题 #anki#
- 数学是否是完备的,即所有的数学命题都可以由一组有限的公理证明与否
- 数学是不是一致的; 简单点理解就是如果我们证明了假命题(eg.1+1=3)那么数学就不是一致的
- 是不是所有命题数学都可以判定
哥德尔给出了不完备性定理证明,认为上述问题1,2不可能同时成立,他给出这样一个命题 #example# #math#
这个命题是不可证的”
这个命题谈论的是它自身,假设该命题为A。现在假设命题A可证,那它就为假(因为它说它不可证),这就意味着证明了假命题——从而算术是不一致的。好了,那我们就假设命题A不可证,这就意味着命题A为真(因为它断言的就是自己不可证),但这样就存在不可证的真命题——算术是不完备的。因此,算术要么不一致,要么不完备。
- 哥德尔的趣事
哥德尔受到时断时续的精神问题困扰,他在维也纳一直待到1940年,最后为了不被征入德军服兵役,移民到美国。(据他的传记作者王浩说,[插图]在准备美国入籍面试时,他发现了美国宪法中的不一致性,结果他的朋友爱因斯坦在陪他去面试时只好不断同他聊天,以引开他的注意力。)
达尔文和孟德尔的思想如何统一
生物的大部分性状都是由许多基因一起决定的,每个基因都有数个不同的等位基因,这种争论才烟消云散。多个不同等位基因会有数量极大的组合可能,从而使得生物的变异像是连续的。生物在基因层面的离散变异会导致表型——基因决定的生理特征(例如高矮、肤色等)——看似连续的变异。人们最终认识到,达尔文与孟德尔的理论并不矛盾,而是互补的。
计算机的自我复制为什么可行
自我复制:计算机不能复制自身;要复制自身就必须包含对自身的描述;而这个描述又包含其本身的描述,这样反复无穷。
自我复制程序,内存中的信息既可以作为指令同时也可以作为数据,用来避免无穷无尽的自我复制
(待续…….)